Statistical mechanics of non-binary networks
Conrad J. Pérez-Vicente
Statistical properties of binary complex networks are well understood and recently many attempts have been made to extend this knowledge to weighted ones. There are, however, subtle yet important considerations to be made regarding the nature of the weights used in this generalization.
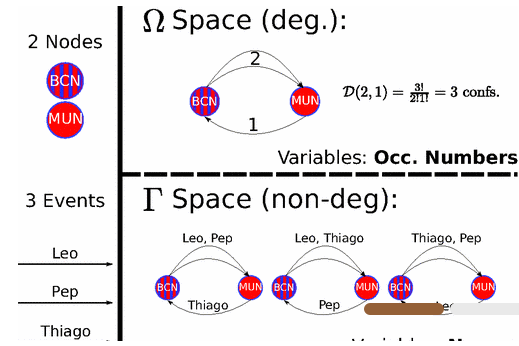
Weights can be either continuous or discrete magnitudes, and in the latter case, they can additionally have undistinguishable or distinguishable nature. Moreover, non-binary adjacency matrices can be constructed in multiple ways such as aggregating multiple layers of information. This "additional" dimension that weights confere to networks makes its study in terms of entropy and randomness an interesting subject. Questions such as: How many (different) network can we build with prescribed properties? Which are the apropriate statistics to model weighted networks? or Can those be uniquely defined? can be then posed.
The way of tackling such problems opens the door to apply many well-known and stablished tools of Classical Statistical mechanics to the study of networks, yet it also offers the possibility to perform a critical review of such tools and to explore the limits of this analogy.


