Multiplex networks
Albert Diaz-Guilera
The Science of Complex Systems is an emergent discipline rather successful in the last years. However, further progress in the physics is hampered by the lack of deep knowledge about how multi-level complex systems organize and operate. Preliminary results show that interactions at different levels behave in a significantly different way than in an isolated level. For example, such dependencies may induce cascading failures and sudden collapses of the entire system. This makes the science of complex networks particularly suitable for the exploration of the many challenges that we face today, including critical infrastructures and communication systems, as well as techno-social and socioeconomic networks.
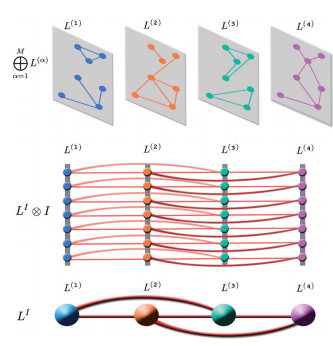
We have been working in the development of a mathematical, computational and algorithmic framework for the study of the physics of multiscale complex systems. The chosen framework consists in a set of layers in such a way that every single layer has exactly the same set of nodes, but they can have different patterns of connectivity. A clear example can be that of social networks, where a layer can be a set of Twitter users having its respective set of following and followed users and another layer can be the same set of Facebook users. A user can have different sets of neighbours in each network because one can think on more familiar or more professional links. But the set of users is exactly the same. In this case, one can imagine that information can flow in any of the two layers and dhifting from one to the other when one of the users decide to do it.
Relevant references
Interplay between social infuence and competitive strategical games in multiplex networks
Roberta Amato, Albert Díaz-Guilera and Kaj-Kolja Kleineberg
Scientific Reports
(2017)
abstract
We present a model that takes into account the coupling between evolutionary game dynamics and social influence. Importantly, social influence and game dynamics take place in different domains, which we model as different layers of a multiplex network. We show that the coupling between these dynamical processes can lead to cooperation in scenarios where the pure game dynamics predicts defection. In addition, we show that the structure of the network layers and the relation between them can further increase cooperation. Remarkably, if the layers are related in a certain way, the system can reach a polarized metastable state. These findings could explain the prevalence of polarization observed in many social dilemmas.
Opinion competition dynamics on multiplex networks
R Amato, N E Kouvaris, M San Miguel and A Díaz-Guilera
New J. Phys
(2017)
abstract
Multilayer and multiplex networks represent a good proxy for the description of social phenomena where social structure is important and can have different origins. Here, we propose a model of opinion competition where individuals are organized according to two different structures in two layers. Agents exchange opinions according to the Abrams–Strogatz model in each layer separately and opinions can be copied across layers by the same individual. In each layer a different opinion is dominant, so each layer has a different absorbing state. Consensus in one opinion is not the only possible stable solution because of the interaction between the two layers. A new mean field solution has been found where both opinions coexist. In a finite system there is a long transient time for the dynamical coexistence of both opinions. However, the system ends in a consensus state due to finite size effects. We analyze sparse topologies in the two layers and the existence of positive correlations between them, which enables the coexistence of inter-layer groups of agents sharing the same opinion.
Pattern formation in multiplex networks
Nikos E. Kouvaris, Shigefumi Hata and Albert Díaz-Guilera
Scientific Reports
(2015)
abstract
The advances in understanding complex networks have generated increasing interest in dynamical processes occurring on them. Pattern formation in activator-inhibitor systems has been studied in networks, revealing differences from the classical continuous media. Here we study pattern formation in a new framework, namely multiplex networks. These are systems where activator and inhibitor species occupy separate nodes in different layers. Species react across layers but diffuse only within their own layer of distinct network topology. This multiplicity generates heterogeneous patterns with significant differences from those observed in single-layer networks. Remarkably, diffusion-induced instability can occur even if the two species have the same mobility rates; condition which can never destabilize single-layer networks. The instability condition is revealed using perturbation theory and expressed by a combination of degrees in the different layers. Our theory demonstrates that the existence of such topology-driven instabilities is generic in multiplex networks, providing a new mechanism of pattern formation.
An algebraic topological method for multimodal brain networks comparisons
Tiago Simas, Mario Chavez, Pablo R. Rodriguez and Albert Diaz-Guilera
Front. Psychol.
(2015)
abstract
Understanding brain connectivity is one of the most important issues in neuroscience. Nonetheless, connectivity data can reflect either functional relationships of brain activities or anatomical connections between brain areas. Although both representations should be related, this relationship is not straightforward. We have devised a powerful method that allows different operations between networks that share the same set of nodes, by embedding them in a common metric space, enforcing transitivity to the graph topology. Here, we apply this method to construct an aggregated network from a set of functional graphs, each one from a different subject. Once this aggregated functional network is constructed, we use again our method to compare it with the structural connectivity to identify particular brain regions that differ in both modalities (anatomical and functional). Remarkably, these brain regions include functional areas that form part of the classical resting state networks. We conclude that our method -based on the comparison of the aggregated functional network- reveals some emerging features that could not be observed when the comparison is performed with the classical averaged functional network.
Diffusion Dynamics on Multiplex Networks
Gomez, S. Albert Diaz-Guilera, J. Gomez-Gardenes, Conrad J. Perez-Vicente, Yamir Moreno, Alex Arenas,
PHYSICAL REVIEW LETTERS
(2013)
abstract
We study the time scales associated with diffusion processes that take place on multiplex networks, i.e., on a set of networks linked through interconnected layers. To this end, we propose the construction of a supra-Laplacian matrix, which consists of a dimensional lifting of the Laplacian matrix of each layer of the multiplex network. We use perturbative analysis to reveal analytically the structure of eigenvectors and eigenvalues of the complete network in terms of the spectral properties of the individual layers. The spectrum of the supra-Laplacian allows us to understand the physics of diffusionlike processes on top of multiplex networks. DOI: 10.1103/PhysRevLett.110.028701
Spectral properties of the Laplacian of a multiplex network
Albert Sole-Ribata, Manlio De Domenico, Nikos E. Kouvaris, Albert Díaz-Guilera, Sergio Gómez and Alex Arenas
Physical Review E
(2013)
abstract
One of the more challenging tasks in the understanding of dynamical properties of models on top of complex networks is to capture the precise role of multiplex topologies. In a recent paper, Gómez et al. [Phys. Rev. Lett. 110, 028701 (2013)], some of the authors proposed a framework for the study of diffusion processes in such networks. Here, we extend the previous framework to deal with general configurations in several layers of networks and analyze the behavior of the spectrum of the Laplacian of the full multiplex. We derive an interesting decoupling of the problem that allow us to unravel the role played by the interconnections of the multiplex in the dynamical processes on top of them. Capitalizing on this decoupling we perform an asymptotic analysis that allow us to derive analytical expressions for the full spectrum of eigenvalues. This spectrum is used to gain insight into physical phenomena on top of multiplex, specifically, diffusion processes and synchronizability.