Stochastic dynamics and extreme time events for socio-economic systems
Josep Perelló
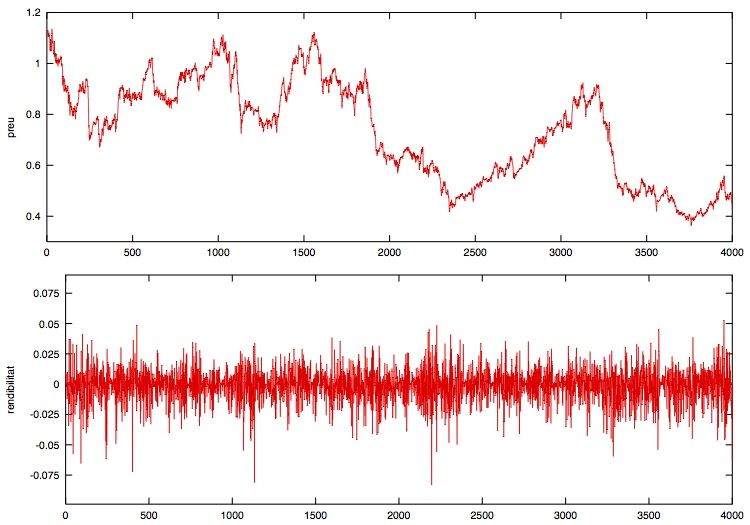
The use of time series analysis and stochastic process modeling in complex systems studies has a long tradition, going back to to the application of Brownian (Gaussian) motion modeling to prices in the Paris stock market by Bachelier in 1900.
These models and the statistics behind are best documented in the study of human activity patterns, and include burstiness, long-range cross-correlation and auto-correlation, and strong non-Gaussanity. We have mostly focussed on those aspects valid for the study of financial markets time series although we also recently also analyzed aspects with crutial interest in the economics of climate change.
During the last decade, the group has focused on a number of major challenges in this area including the alignment between theoretical and empirical analysis of extreme events, data driven probability inference in time-series and direct parameter estimation in agent-based modelling.
We have solved and analyzed a large class of stochastic models. Some of them are defined in terms of a Langevin equation or a stochastic differential equation and, in some cases, we also treat multidimensional and coupled diffusion processes. Another approach we have explored is by means of the so-called Continuous Time Rando Walk framework.
Relevant references
Fractional telegrapher’s equation from fractional persistent random walks
J. Masoliver
Phys. Rev E
(2016)
abstract
We generalize the telegrapher’s equation to allow for anomalous transport. We derive the space-time fractional telegrapher’s equation using the formalism of the persistent random walk in continuous time. We also obtain the characteristic function of the space-time fractional process and study some particular cases and asymptotic approximations. Similarly to the ordinary telegrapher’s equation, the time-fractional equation also presents distinct behaviors for different time scales. Specifically, transitions between different subdiffusive regimes or from superdiffusion to subdiffusion are shown by the fractional equation as time progresses.
Quantum walk with a general coin: exact solution and asymptotic properties
Miquel Montero
QUANTUM INFORMATION PROCESSING
(2015)
abstract
In this paper, we present closed-form expressions for the wave function that governs the evolution of the discrete-time quantum walk on the line when the coin operator is arbitrary. The formulas were derived assuming that the walker can either remain put in the place or proceed in a fixed direction but never move backward, although they can be easily modified to describe the case in which the particle can travel in both directions. We use these expressions to explore properties ofmagnitudes associated to the process, as the probability mass function or the probability current, even though we also consider the asymptotic behavior of the exact solution. Within this approximation, we will estimate upper and lower bounds, examine the origins of an emerging approximate symmetry, and deduce the general form of the stationary probability density of the relative location of the walker.
Extreme values and the level-crossing problem: An application to the Feller process
Jaume Masoliver,
PHYSICAL REVIEW E
(2014)
abstract
We review the question of the extreme values attained by a random process. We relate it to level crossings to one boundary (first-passage problems) as well as to two boundaries (escape problems). The extremes studied are the maximum, the minimum, the maximum absolute value, and the range or span. We specialize in diffusion processes and present detailed results for the Wiener and Feller processes.
Invariance in quantum walks with time-dependent coin operators
Miquel Montero,
PHYSICAL REVIEW A
(2014)
abstract
This paper unveils some features of a discrete-time quantum walk on the line whose coin depends on the temporal variable. After considering the most general form of the unitary coin operator, it focuses on the role played by the two phase factors that one can incorporate there, and shows how both terms influence the evolution of the system. A closer analysis reveals that the probabilistic properties of the motion of the walker remain unaltered when the update rule of these phases is chosen adequately. This invariance is based on a symmetry with consequences not yet fully explored.
The Level-Crossing Problem: First-Passage, Escape and Extremes
Jaume Masoliver,
FLUCTUATION AND NOISE LETTERS
(2014)
abstract
We review the level-crossing problem which includes the first-passage and escape problems as well as the theory of extreme values (the maximum, the minimum, the maximum absolute value and the range or span). We set the definitions and general results and apply them to one-dimensional diffusion processes with explicit results for the Brownian motion and the Ornstein-Uhlenbeck (OU) process.
Monotonic continuous-time random walks with drift and stochastic reset events
Miquel Montero, Javier Villarroel,
PHYSICAL REVIEW E
(2013)
abstract
In this paper we consider a stochastic process that may experience random reset events which suddenly bring the system to the starting value and analyze the relevant statistical magnitudes. We focus our attention on monotonic continuous-time random walks with a constant drift: The process increases between the reset events, either by the effect of the random jumps, or by the action of the deterministic drift. As a result of all these combined factors interesting properties emerge, like the existence (for any drift strength) of a stationary transition probability density function, or the faculty of the model to reproduce power-law-like behavior. General formulas for two extreme statistics, the survival probability, and the mean exit time are also derived. To corroborate in an independent way the results of the paper, Monte Carlo methods were used. These numerical estimations are in full agreement with the analytical predictions. DOI: 10.1103/PhysRevE.87.012116
Unidirectional quantum walks: Evolution and exit times
Miquel Montero,
PHYSICAL REVIEW A
(2013)
abstract
In this paper we focus our attention on a particle that follows a unidirectional quantum walk, an alternative version of the currently widespread discrete-time quantum walk on a line. Here the walker at each time step can either remain in place or move in a fixed direction, e.g., rightward or upward. While both formulations are essentially equivalent, the present approach leads us to consider discrete Fourier transforms, which eventually results in obtaining explicit expressions for the wave functions in terms of finite sums and allows the use of efficient algorithms based on the fast Fourier transform. The wave functions here obtained govern the probability of finding the particle at any given location but determine as well the exit-time probability of the walker from a fixed interval, which is also analyzed.
First-passage and escape problems in the Feller process
Jaume Masoliver, Josep Perello,
PHYSICAL REVIEW E
(2012)
abstract
The Feller process is an one-dimensional diffusion process with linear drift and state-dependent diffusion coefficient vanishing at the origin. The process is positive definite and it is this property along with its linear character that have made Feller process a convenient candidate for the modeling of a number of phenomena ranging from single-neuron firing to volatility of financial assets. While general properties of the process have long been well known, less known are properties related to level crossing such as the first-passage and the escape problems. In this work we thoroughly address these questions.
Maximum likelihood approach for several stochastic volatility models
Jordi Camprodon, Josep Perello,
JOURNAL OF STATISTICAL MECHANICS-THEORY AND EXPERIMENT
(2012)
abstract
Volatility measures the amplitude of price fluctuations. Despite it being one of the most important quantities in finance, volatility is not directly observable. Here we apply a maximum likelihood method which assumes that price and volatility follow a two-dimensional diffusion process where volatility is the stochastic diffusion coefficient of the log-price dynamics. We apply this method to the simplest versions of the expOU, the OU and the Heston stochastic volatility models and we study their performance in terms of the log-price probability, the volatility probability, and its Mean First-Passage Time. The approach has some predictive power on the future returns amplitude by only knowing the current volatility. The assumed models do not consider long-range volatility autocorrelation and the asymmetric return-volatility cross-correlation but the method still yields very naturally these two important stylized facts. We apply the method to different market indices and with a good performance in all cases.
Scaling properties and universality of first-passage-time probabilities in financial markets
Josep Perello, Mario Gutierrez-Roig, Jaume Masoliver,
PHYSICAL REVIEW E
(2011)
abstract
Financial markets provide an ideal frame for the study of crossing or first-passage time events of non-Gaussian correlated dynamics, mainly because large data sets are available. Tick-by-tick data of six futures markets are herein considered, resulting in fat-tailed first-passage time probabilities. The scaling of the return with its standard deviation collapses the probabilities of all markets examined-and also for different time horizons-into single curves, suggesting that first-passage statistics is market independent (at least for high-frequency data). On the other hand, a very closely related quantity, the survival probability, shows, away from the center and tails of the distribution, a hyperbolic t(-1/2) decay typical of a Markovian dynamics, albeit the existence of memory in markets. Modifications of the Weibull and Student distributions are good candidates for the phenomenological description of first-passage time properties under certain regimes. The scaling strategies shown may be useful for risk control and algorithmic trading.
Parrondo-like behavior in continuous-time random walks with memory
Miquel Montero,
PHYSICAL REVIEW E
(2011)
abstract
The continuous-time random walk (CTRW) formalism can be adapted to encompass stochastic processes with memory. In this paper we will show how the random combination of two different unbiased CTRWs can give rise to a process with clear drift, if one of them is a CTRW with memory. If one identifies the other one as noise, the effect can be thought of as a kind of stochastic resonance. The ultimate origin of this phenomenon is the same as that of the Parrondo paradox in game theory.
The impact of heterogeneous trading rules on the limit order book and order flows
Carl Chiarella, Giulia Iori, Josep Perello,
JOURNAL OF ECONOMIC DYNAMICS & CONTROL
(2009)
abstract
In this paper we develop a model of an order-driven market where traders set bids and asks and post market or limit orders according to exogenously fixed rules. Agents are assumed to have three components of the expectation of future asset returns, namely fundamentalist, chartist and noise trader. Furthermore agents differ in the characteristics describing these components, such as time horizon. risk aversion and the weights given to the various components. The model developed here extends a great deal of earlier literature in that the order submissions of agents are determined by utility maximisation, rather than the mechanical unit order size that is commonly assumed. In this way the order flow is better related to the ongoing evolution of the market. For the given market structure we analyze the impact of the three components of the trading strategies on the statistical properties of prices and order flows and observe that it is the chartist strategy that is mainly responsible of the fat tails and clustering in the artificial price data generated by the model. The paper provides further evidence that large price changes are likely to be generated by the presence of large gaps in the book. (C) 2008 Elsevier B.V. All rights reserved.
Perpetual American vanilla option pricing under single regime change risk: an exhaustive study
Miquel Montero,
JOURNAL OF STATISTICAL MECHANICS-THEORY AND EXPERIMENT
(2009)
abstract
Perpetual American options are financial instruments that can be readily exercised and do not mature. In this paper we study in detail the problem of pricing this kind of derivatives, for the most popular favour, within a framework in which some of the properties-volatility and dividend policy-of the underlying stock can change at a random instant of time but in such a way that we can forecast their final values. Under this assumption we can model actual market conditions because most relevant facts usually entail sharp predictable consequences. The effect of this potential risk on perpetual American vanilla options is remarkable: the very equation that will determine the fair price depends on the solution to be found. Sound results are found under the optics both of finance and physics. In particular, a parallelism among the overall outcome of this problem and a phase transition is established.