New paper in PNAS
M. B. publications 2021/06/21
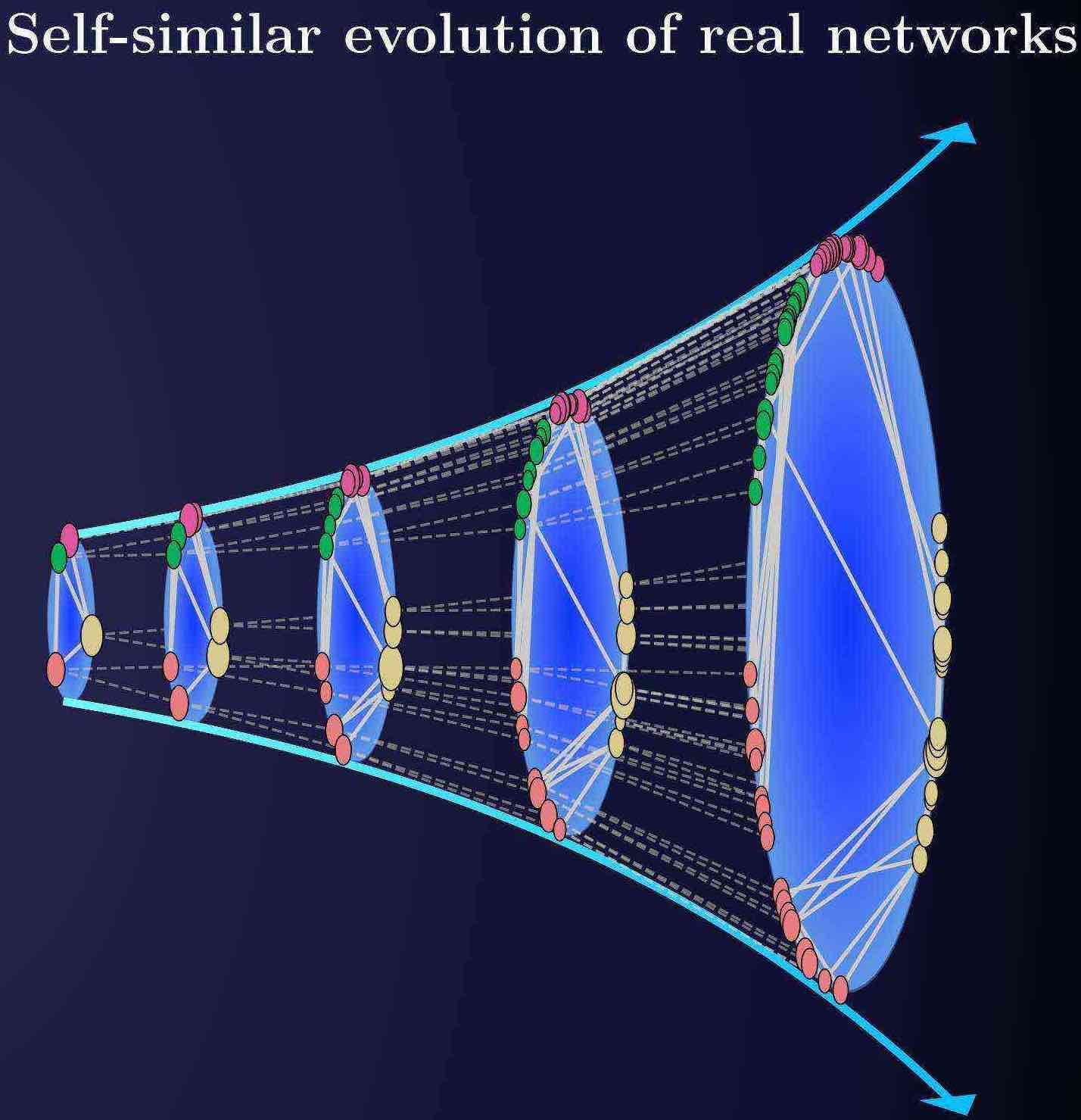
Scaling up real networks by geometric branching growth
Branching processes underpin the complex evolution of manyreal systems. However, network models typically describe net-work growth in terms of a sequential addition of nodes. Here,we measured the evolution of real networks—journal cita-tions and international trade—over a 100-y period and foundthat they grow in a self-similar way that preserves their struc-tural features over time. This observation can be explained bya geometric branching growth model that generates a mul-tiscale unfolding of the network by using a combination ofbranching growth and a hidden metric space approach. Ourmodel enables multiple practical applications, including thedetection of optimal network size for maximal response to anexternal influence and a finite-size scaling analysis of criticalbehavior. Read the paper.